
(Eds.) "Chapter 14: Analysing categorical data: Log-linear analysis". Scaling log-linear analysis to high-dimensional data (PDF). Log-Linear Models and Logistic Regression (2nd ed.). An Introduction to Categorical Data Analysis (2nd ed.).
Discovering statistics using SPSS (2nd ed.). Statistical methods for psychology (7th ed.). IBM SPSS Statistics with the GENLOG procedure ( usage)įor datasets with hundreds of variables – decomposable models.R with the loglm function of the MASS package (see tutorial).
Odds ratio spss software#
Software For datasets with a few variables – general log-linear models Odds ratios are not affected by unequal marginal distributions. Odds ratios are independent of the sample size Ģ.

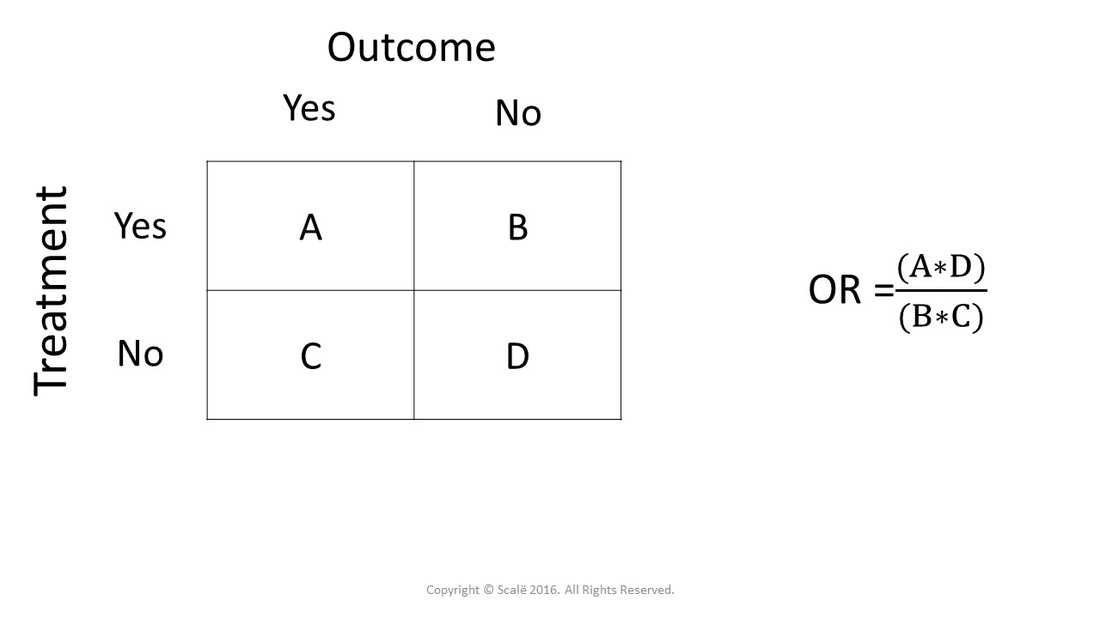
Odds ratios are preferred over chi-square statistics for two main reasons: ġ. To compare effect sizes of the interactions between the variables, odds ratios are used. įor example, if one is examining the relationship among four variables, and the model of best fit contained one of the three-way interactions, one would examine its simple two-way interactions at different levels of the third variable. To conduct chi-square analyses, one needs to break the model down into a 2 × 2 or 2 × 1 contingency table. Once the model of best fit is determined, the highest-order interaction is examined by conducting chi-square analyses at different levels of one of the variables. Else, if the chi-square difference is larger than the critical value, the less parsimonious model is preferred. If the chi-square difference is smaller than the chi-square critical value, the new model fits the data significantly better and is the preferred model. This value is then compared to the chi-square critical value at their difference in degrees of freedom. The chi-square difference test is computed by subtracting the likelihood ratio chi-square statistics for the two models being compared. When two models are nested, models can also be compared using a chi-square difference test. The highest ordered interactions are no longer removed when the likelihood ratio chi-square statistic becomes significant. Specifically, at each stage, after the removal of the highest ordered interaction, the likelihood ratio chi-square statistic is computed to measure how well the model is fitting the data. Log-linear analysis starts with the saturated model and the highest order interactions are removed until the model no longer accurately fits the data. If the likelihood ratio chi-square statistic is significant, then the model does not fit well (i.e., calculated expected frequencies are not close to observed frequencies).īackward elimination is used to determine which of the model components are necessary to retain in order to best account for the data. If the likelihood ratio chi-square statistic is non-significant, then the model fits well (i.e., calculated expected frequencies are close to observed frequencies). The model fits well when the residuals (i.e., observed-expected) are close to 0, that is the closer the observed frequencies are to the expected frequencies the better the model fit. Moreover, being completely determined by its two-factor terms, a graphical model can be represented by an undirected graph, where the vertices represent the variables and the edges represent the two-factor terms included in the model.Ī log-linear model is decomposable if it is graphical and if the corresponding graph is chordal. Īs a direct-consequence, graphical models are hierarchical. Graphical model Ī log-linear model is graphical if, whenever the model contains all two-factor terms generated by a higher-order interaction, the model also contains the higher-order interaction. These models contain all the lower order interactions and main effects of the interaction to be examined. Log-linear analysis models can be hierarchical or nonhierarchical. Log-linear analysis uses a likelihood ratio statistic X 2 the relative weight of each variable. 7.2 For datasets with hundreds of variables – decomposable models.7.1 For datasets with a few variables – general log-linear models.


 0 kommentar(er)
0 kommentar(er)
